Pochodna – w analizie matematycznej miara szybkości zmian wartości funkcji względem zmian jej argumentów
Pochodna funkcji zmiennej rzeczywistej o wartościach rzeczywistych
Niech 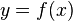 będzie funkcją rzeczywistą zmiennej rzeczywistej
będzie funkcją rzeczywistą zmiennej rzeczywistej  określoną w otoczeniu punktu
określoną w otoczeniu punktu  [2].Pochodną funkcji f(x) w punkcie
[2].Pochodną funkcji f(x) w punkcie  nazywamy granicę (o ile istnieje):
nazywamy granicę (o ile istnieje):
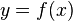 będzie funkcją rzeczywistą zmiennej rzeczywistej
będzie funkcją rzeczywistą zmiennej rzeczywistej  określoną w otoczeniu punktu
określoną w otoczeniu punktu  [2].Pochodną funkcji f(x) w punkcie
[2].Pochodną funkcji f(x) w punkcie  nazywamy granicę (o ile istnieje):
nazywamy granicę (o ile istnieje):
Co symbolicznie zapisuje się w jednej z postaci:
 [3],
[3],
We wzorze tym:
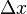 jest przyrostem zmiennej niezależnej x,
jest przyrostem zmiennej niezależnej x, jest przyrostem zmiennej zależnej y,
jest przyrostem zmiennej zależnej y,- Wyrażenie
 nazywa się ilorazem różnicowym; jest on funkcją przyrostu zmiennej niezależnej.
nazywa się ilorazem różnicowym; jest on funkcją przyrostu zmiennej niezależnej.
Jeżeli przyjmie się, że 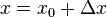 , to pochodną w punkcie
, to pochodną w punkcie  można zapisać następująco:
można zapisać następująco:
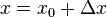 , to pochodną w punkcie
, to pochodną w punkcie  można zapisać następująco:
można zapisać następująco: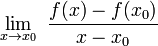 .
.
Często w publikacjach przyrost 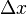 oznacza się literą h. Wtedy pochodna jest równa:
oznacza się literą h. Wtedy pochodna jest równa:
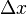 oznacza się literą h. Wtedy pochodna jest równa:
oznacza się literą h. Wtedy pochodna jest równa: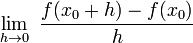 [4].
[4].
Jeśli funkcja 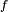 ma pochodną dla każdego elementu swej dziedziny
ma pochodną dla każdego elementu swej dziedziny  to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji
to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji 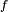 lub krótko: pochodną
lub krótko: pochodną  w dalszej części artykułu będzie ono oznaczane symbolem
w dalszej części artykułu będzie ono oznaczane symbolem  – pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób
– pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób  oznaczać będzie pochodną funkcji
oznaczać będzie pochodną funkcji 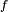 dla argumentu
dla argumentu  w tym wypadku
w tym wypadku  również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
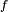 ma pochodną dla każdego elementu swej dziedziny
ma pochodną dla każdego elementu swej dziedziny  to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji
to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji 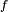 lub krótko: pochodną
lub krótko: pochodną  w dalszej części artykułu będzie ono oznaczane symbolem
w dalszej części artykułu będzie ono oznaczane symbolem  – pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób
– pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób  oznaczać będzie pochodną funkcji
oznaczać będzie pochodną funkcji 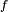 dla argumentu
dla argumentu  w tym wypadku
w tym wypadku  również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.Własności funkcji pochodne
:iloczyn pochodnej przez stałą,
- pochodną sumy funkcji (addytywność),
 ;
;
- pochodną iloczynu funkcji (reguła Leibniza),
- pochodną złożenia funkcji (reguła łańcuchowa),
- pochodną funkcji odwrotnej,
- pochodną odwrotności funkcji (reguła odwrotności),
- pochodną ilorazu funkcji (reguła ilorazu),
 .
.
Przykłady
funkcje stałe i funkcje potęgowe,Istnieje pewien zestaw funkcji uważanych za elementarne, które wykorzystuje się do obliczania pochodnych bardziej skomplikowanych funkcji i ich złożeń; niech
 oznacza stałą, zaś
oznacza stałą, zaś  będzie liczbą naturalną, wówczas:
będzie liczbą naturalną, wówczas:-
- funkcje wykładnicze[8] i logarytmiczne[9]
- funkcje trygonometryczne[10],
- funkcje cyklometryczne[11],
wszędzie, gdzie powyższe wzory mają sens.
Pochodne wyższego rzędu
Jeżeli pochodna funkcji  i stnieje w każdym punkcie przedziału otwartego (a, b), to otrzymujemy funkcję
i stnieje w każdym punkcie przedziału otwartego (a, b), to otrzymujemy funkcję  , taką że
, taką że
 dla x ∈ (a, b).
dla x ∈ (a, b).
Funkcję tę nazywamy pierwszą pochodną funkcji f. Ta funkcja może być również różniczkowalna w każdym punkcie przedziału (a, b). Różniczkując ją, otrzymujemy drugą pochodną funkcjif:
 dla x ∈ (a, b).
dla x ∈ (a, b).
Oznaczamy to następująco:
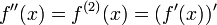 lub
lub  .
.
Ogólnie pochodną rzędu n określamy rekurencyjnie:
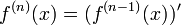 lub
lub  [12].
[12].
Przykłady




- n-tą pochodną iloczynu funkcji można wyrazić za pomocą pochodnych czynników oraz współczynników Newtona wzorem:

Pochodna a monotoniczność funkcji, ekstrema i punkty przegięcia
Z twierdzenia Lagrange'a wynikają następujące własności pochodnej
- Jeżeli funkcja
 jest różniczkowalna, to
jest różniczkowalna, to
- Jeśli
 , to f jest funkcją rosnącą na (a, b).
, to f jest funkcją rosnącą na (a, b). - Jeśli
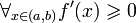 , to f jest funkcją niemalejącą na (a, b).
, to f jest funkcją niemalejącą na (a, b). - Jeśli
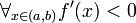 , to f jest funkcją malejącą na (a, b).
, to f jest funkcją malejącą na (a, b). - Jeśli
 , to f jest funkcją nierosnącą na (a, b).
, to f jest funkcją nierosnącą na (a, b). - Jeśli
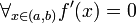 , to f jest funkcją stałą na (a, b).
, to f jest funkcją stałą na (a, b).
- Jeśli
Z własności tych wynika, że ważnymi punktami dziedziny funkcji różniczkowalnej są miejsca zerowe jej pochodnej. Ponieważ funkcja różniczkowalna jest funkcją ciągłą[23], więc jeśli funkcja jest określona na przedziale otwartym, to zbiory rozwiązań nierówności i
i  są sumami przedziałów otwartych.Zbiór miejsc zerowych pochodnej jest zbiorem domkniętym. Miejsca zerowe pierwszej pochodnej są bardzo ważne w badaniu funkcji. W praktyce obliczeniowej funkcje na ogół mają skończoną lub przeliczalną liczbę miejsc zerowych, które dzielą dziedzinę na przedziały otwarte, w których pochodna jest stale dodatnia lub stale ujemna. Wtedy każde miejsce zerowe albo oddziela dwa przedziały, na których pochodna przyjmuje jednakowe znaki, albo różne znaki. Stąd wynikają następujące definicje.
są sumami przedziałów otwartych.Zbiór miejsc zerowych pochodnej jest zbiorem domkniętym. Miejsca zerowe pierwszej pochodnej są bardzo ważne w badaniu funkcji. W praktyce obliczeniowej funkcje na ogół mają skończoną lub przeliczalną liczbę miejsc zerowych, które dzielą dziedzinę na przedziały otwarte, w których pochodna jest stale dodatnia lub stale ujemna. Wtedy każde miejsce zerowe albo oddziela dwa przedziały, na których pochodna przyjmuje jednakowe znaki, albo różne znaki. Stąd wynikają następujące definicje.- Funkcja
 przyjmuje w punkcie x0 maksimum, jeśli istnieje takie otoczenie tego punktu
przyjmuje w punkcie x0 maksimum, jeśli istnieje takie otoczenie tego punktu 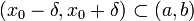 , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 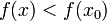 [24].
[24].
Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:- dodatnia w przedziale
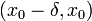 ,
, - równa zero w x0,
- ujemna w przedziale

to funkcja f ma w x0 maksimum.- Funkcja
 przyjmuje w punkcie x0 minimum, jeśli istnieje takie otoczenie tego punktu
przyjmuje w punkcie x0 minimum, jeśli istnieje takie otoczenie tego punktu 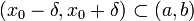 , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność  [25].
[25].
Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:- ujemna w przedziale
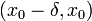 ,
, - równa zero w x0,
- dodatnia w przedziale

to funkcja f ma w x0 minimum.Minima i maksima funkcji nazywamy jej ekstremami.- Funkcja
 ma w punkcie x0 punkt przegięcia, jeśli jej pochodna jest:
ma w punkcie x0 punkt przegięcia, jeśli jej pochodna jest:
- równa zero w x0,
- albo dodatnia, albo ujemna w zbiorze
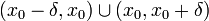 .
.
Schemat badania zmienności funkcji\
Przed narysowaniem wykresu funkcji
 należy[26]:
należy[26]:- Znaleźć dziedzinę funkcji. Znaleźć granice funkcji w punktach brzegu dziedziny.
- Znaleźć miejsca zerowe pochodnej funkcji, punkty, w których pochodna funkcji nie istnieje lub jest równa ±∞. Obliczyć wartości funkcji w tych punktach i stwierdzić, czy w tych punktach funkcja przyjmuje minimum lub maksimum.
- Na każdym z przedziałów wyznaczonych przez miejsca zerowe pochodnej ustalić, czy funkcja jest rosnąca, czy malejąca.
- Zbadać istnienie punktów przegięcia funkcji.
- Rozwiązać, jeśli to możliwe, równanie
 oraz ustalić przedziały, w których funkcja ma stały znak.
oraz ustalić przedziały, w których funkcja ma stały znak. - Znaleźć asymptoty funkcji.
Funkcje wielu zmiennych
Pochodne cząstkowe
W przypadku funkcji wielu zmiennych
 możliwe jest ustalenie
możliwe jest ustalenie  jej argumentów i traktowanie jej jako funkcji jednej zmiennej – pochodną względem tej zmiennej nazywa się „pochodną cząstkową”. Jeśli
jej argumentów i traktowanie jej jako funkcji jednej zmiennej – pochodną względem tej zmiennej nazywa się „pochodną cząstkową”. Jeśli  gdzie
gdzie  to pochodną cząstkową funkcji
to pochodną cząstkową funkcji 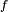 względem jej
względem jej  -tej współrzędnej
-tej współrzędnej  nazywa się wartość granicyo ile istnieje i jest skończona. W zapisie wektorowym powyższą granicę można zapisać wzoremgdzie
nazywa się wartość granicyo ile istnieje i jest skończona. W zapisie wektorowym powyższą granicę można zapisać wzoremgdzie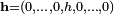 jest wektorem o jedynej niezerowej współrzędnej
jest wektorem o jedynej niezerowej współrzędnej  -tej.Powyższą definicję można rozszerzyć zauważając, że
-tej.Powyższą definicję można rozszerzyć zauważając, że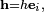 gdzie
gdzie  jest wektorem bazy standardowej przestrzeni
jest wektorem bazy standardowej przestrzeni 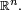 Wybranie dowolnego wektora jednostkowego
Wybranie dowolnego wektora jednostkowego  zamiast wektora bazy prowadzi do definicji pochodnej kierunkowej wzdłuż
zamiast wektora bazy prowadzi do definicji pochodnej kierunkowej wzdłuż  mianowicie:Jeśli
mianowicie:Jeśli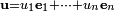 jest wektorem jednostkowym, to pochodna kierunkowa funkcji
jest wektorem jednostkowym, to pochodna kierunkowa funkcji 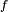 wzdłuż
wzdłuż  jest równa kombinacji liniowej pochodnych cząstkowych funkcji
jest równa kombinacji liniowej pochodnych cząstkowych funkcji 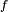 o współczynnikach
o współczynnikach 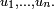
Pochodne zupełne
 Dowolną funkcję
Dowolną funkcję można rozłożyć na funkcje współrzędnych
można rozłożyć na funkcje współrzędnych  przyjmując
przyjmując 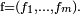 Jeżeli funkcje te są różniczkowalne w każdym kierunku, co jest równoważne istnieniu ich wszystkich pochodnych cząstkowych, to funkcję
Jeżeli funkcje te są różniczkowalne w każdym kierunku, co jest równoważne istnieniu ich wszystkich pochodnych cząstkowych, to funkcję  nazywa się różniczkowalną w słabym sensie[27]; przedstawieniem tej pochodnej we współrzędnych za pomocą odpowiadającej jej macierzy przekształcenia liniowego jest tzw.macierz Jacobiego.Mogłoby się wydawać, że definicja słabej pochodnej jest w zupełności zadowalająca, jednak w przypadku funkcji wielowymiarowych należy zwrócić uwagę na zjawiska związane z większą liczbą wymiarów: istnieją przykładowo funkcje, które mają pochodne we wszystkich kierunkach (równoważnie: mają wszystkie pochodne cząstkowe, zob. ostatni ustęp poprzedniej sekcji), czyli wzdłuż prostych, lecz nie mają pochodnych wzdłuż innych krzywych – problem ten nie istnieje w przypadku funkcji zmiennej rzeczywistej, gdzie granicę można obliczać wyłącznie wzdłuż krzywych leżących wyłącznie na prostej.Definicja pochodnej funkcji wielu zmiennych
nazywa się różniczkowalną w słabym sensie[27]; przedstawieniem tej pochodnej we współrzędnych za pomocą odpowiadającej jej macierzy przekształcenia liniowego jest tzw.macierz Jacobiego.Mogłoby się wydawać, że definicja słabej pochodnej jest w zupełności zadowalająca, jednak w przypadku funkcji wielowymiarowych należy zwrócić uwagę na zjawiska związane z większą liczbą wymiarów: istnieją przykładowo funkcje, które mają pochodne we wszystkich kierunkach (równoważnie: mają wszystkie pochodne cząstkowe, zob. ostatni ustęp poprzedniej sekcji), czyli wzdłuż prostych, lecz nie mają pochodnych wzdłuż innych krzywych – problem ten nie istnieje w przypadku funkcji zmiennej rzeczywistej, gdzie granicę można obliczać wyłącznie wzdłuż krzywych leżących wyłącznie na prostej.Definicja pochodnej funkcji wielu zmiennych stanowiącą rozwiązanie tego problemu naśladuje definicję „różniczkową” dla funkcji rzeczywistej (zob.Związek z różniczką). Pochodną w mocnym sensie[28] funkcji
stanowiącą rozwiązanie tego problemu naśladuje definicję „różniczkową” dla funkcji rzeczywistej (zob.Związek z różniczką). Pochodną w mocnym sensie[28] funkcji  dla argumentu punktowego
dla argumentu punktowego 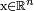 nazywa się takie przekształcenie liniowe
nazywa się takie przekształcenie liniowe  dla którego zachodzigdzie
dla którego zachodzigdzie oznacza moduł odpowiednich wektorów; odwzorowanie
oznacza moduł odpowiednich wektorów; odwzorowanie  podobnie jak w przypadku jednowymiarowym, nazywa się różniczką (w mocnym sensie) funkcji
podobnie jak w przypadku jednowymiarowym, nazywa się różniczką (w mocnym sensie) funkcji  [29]. Rolę funkcji pochodnej pełni tu więc odwzorowanie
[29]. Rolę funkcji pochodnej pełni tu więc odwzorowanie  przestrzeni współrzędnych w przestrzeń liniową przekształceń liniowych (por. przestrzeń funkcyjna przekształceń liniowych) dane wzorem
przestrzeni współrzędnych w przestrzeń liniową przekształceń liniowych (por. przestrzeń funkcyjna przekształceń liniowych) dane wzorem  tj. przypisujące punktowi przekształcenie liniowe.Istnienie pochodnej w silnym sensie pochodnej pociąga istnienie pochodnej w słabym sensie; jeżeli jednak funkcja jest różniczkowalna w słabym sensie i wszystkie jej pochodne cząstkowe (kierunkowe) są ciągłe, to funkcja jest różniczkowalna w silnym sensie w sposób ciągły (tzn. jest klasy
tj. przypisujące punktowi przekształcenie liniowe.Istnienie pochodnej w silnym sensie pochodnej pociąga istnienie pochodnej w słabym sensie; jeżeli jednak funkcja jest różniczkowalna w słabym sensie i wszystkie jej pochodne cząstkowe (kierunkowe) są ciągłe, to funkcja jest różniczkowalna w silnym sensie w sposób ciągły (tzn. jest klasy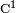 ). Oba rodzaje pochodnych mają wiele własności pochodnej funkcji rzeczywistej, np.liniowość, czy zachodzenie reguły łańcuchowej. Bezpośrednie generalizacje pojęć pochodnych w słabym/silnym sensie, tj. pochodne Gâteaux/Frécheta, opisano w Uogólnieniach.zródło: http://pl.wikipedia.org/wiki/Pochodna
). Oba rodzaje pochodnych mają wiele własności pochodnej funkcji rzeczywistej, np.liniowość, czy zachodzenie reguły łańcuchowej. Bezpośrednie generalizacje pojęć pochodnych w słabym/silnym sensie, tj. pochodne Gâteaux/Frécheta, opisano w Uogólnieniach.zródło: http://pl.wikipedia.org/wiki/Pochodna- Jeżeli funkcja



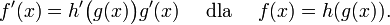
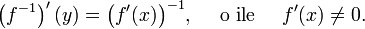
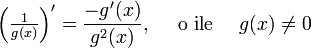






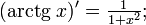


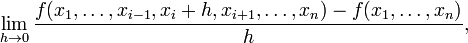


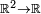 ją opisująca przyjmujemaksimum: warunkiem koniecznym jego istnienia jest znikanie pochodnej (w słabym/silnym sensie) wspomnianej funkcji.
ją opisująca przyjmujemaksimum: warunkiem koniecznym jego istnienia jest znikanie pochodnej (w słabym/silnym sensie) wspomnianej funkcji.