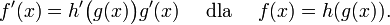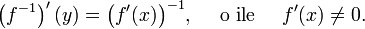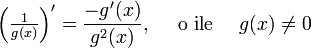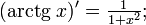Uniwersytet Technologiczno-Humanistyczny
Analiza matematyczna - zespół teorii obejmujący wiele ważnych działów matematyki.
Początkowo analiza matematyczna obejmowała jedynie to, co dzisiaj nazywamy rachunkiem różniczkowym i całkowym. Jej rozwój zainicjowały prace Leibniza i Newtona z początku XVII wieku.
Z czasem rachunek różniczkowy i całkowy, ograniczający się wcześniej do kartezjańskich przestrzeni rzeczywistych, objął swoim zakresem inne przestrzenie: przestrzenie zespolone (teoria funkcji holomorficznych), przestrzenie Banacha i Hilberta (wraz z odpowiadającymi im teoriami) oraz bardziej zaawansowane twory geometryczne (na przykład rozmaitości różniczkowalne).
zródlo: http://pl.wikipedia.org/wiki/Analiza_matematyczna
Algebra liniowa – dział algebry zajmujący się badaniem przestrzeni liniowych oraz ich homomorfizmów, tj. przekształceń liniowych. Algebra liniowa skupia się głównie na badaniu przestrzeni skończenie wymiarowych nad ciałami lub ogólniej, pierścieniami. Do algebry liniowej można zaliczyć także teorię form kwadratowych, macierzy, przekształceń półtora- i wieloliniowych. Dziedzina ta wyrosła w sposób naturalny na gruncie badania układów równań liniowych.
Algebra liniowa ma liczne zastosowania zarówno w matematyce (np. równania różniczkowe, programowanie liniowe), jak i poza nią, np. w ekonomii metody przez nią wypracowane są stosowane do skutecznego modelowania i rozwiązywania problemów związanych z alokacją zasobów.
zródło: http://pl.wikipedia.org/wiki/Algebra_liniowa
Analiza matematyczna i Algebra - Piotrek
sobota, 19 stycznia 2013
piątek, 18 stycznia 2013
Informacje o wykładowcy
Ihor Wasyljowycz Ohirko, ukr. Ігор Васильович Огірко (ur. 14 kwietnia 1952 roku w Jeziernej) – doktor nauk fizyczno-matematycznych, profesor Katedry Wydań Elektronicznych Ukraińskiej Akademii Drukarstwa.
Biografia
Ihor Ohirko urodził się 14 kwietnia 1952 roku w Jeziernej (obwód tarnopolski) na Ukrainie. Jego rodzice, Wasyl i Teodora, byli nauczycielami. Do szkoły uczęszczał we wsi Pidbirci, następnie do szkoły średniej nr 11 we Lwowie, którą ukończył w 1969 roku. Studiował na kierunku techniczno-matematycznym na Uniwersytecie im. Iwana Franka we Lwowie. W 1974 roku, po ukończeniu studiów, został skierowany do pracy w charakterze pracownika naukowego do Instytutu Matematyki we Lwowie, gdzie prowadził badania w zakresie metod matematycznych teorii pola. Jednocześnie wykładał informatykę na Uniwersytecie Lwowskim.
W 1978 roku w Instytucie Stosowanych Problemów Mechaniki i Matematyki obronił dysertację na stopień kandydata nauk. Praca została napisana na temat mechaniki deformowanego ciała twardego i powstała pod kierunkiem Jarosława Buraka. Po obronie Ohirko kontynuując pracę w Instytucie Matematyki awansował na kierownika Wydziału Metod Liczbowych w Mechanice i Matematyce Narodowej Akademii Nauk Ukrainy (ukr. ОЦ ІППММ АН України). W okresie kierowania placówką zajmował się fizycznymi i geometrycznymi modelami nieliniowej termosprężystości ciał przy wykorzystaniu rozmaitych metod optymizacji. Wyniki swoich badań zawarł w rozprawie doktorskiej Mechanika deformowanego ciała twardego (ukr. Механіка деформованого твердого тіла), którą obronił w 1989 roku na Kazańskim Uniwersytecie Państwowym.
Od roku 1990 pracuje w Ukraińskim Instytucie Poligraficznym im. Iwana Fedorowa. W latach 1992–1998 kierował Katedrą Matematyki Stosowanej tego instytutu, a w 2002 roku został profesorem Katedry Wydawnictw Elektronicznych. W latach 2003–2008 pełnił funkcję przewodniczącego państwowej komisji egzaminacyjnej Uniwersytetu im. Iwana Franka we Lwowie w dziedzinie matematyki stosowanej i cybernetyki ekonomicznej. Ponadto uczestniczył w pracach rad naukowych oceniających kandydackie i doktorskie dysertacje, które powstawały na Ukraińskiej Akademii Drukarstwa, Politechnice Lwowskiej, Uniwersytecie im. Iwana Franka. Wykłada także na Wydziale Informatyki i Matematyki Uniwersytetu Technologiczno-Humanistycznego im. Kazimierza Pułaskiego w Radomiu.
Ohirko jest autorem 156 publikacji naukowych, w tym 3 monografii i 59 artykułów naukowych. Jest stałym członkiem kolegiów redakcyjnych dwóch serii wydawniczych: Poligrafia a sprawa wydawnicza (ukr. Поліграфія і видавнича справа) oraz Naukowe zapiski Ukraińskiej Akademii Drukarstwa(ukr. Наукові записки Української академії друкарства).
W 2005 roku za zasługi dla narodu ukraińskiego został nagrodzony dyplomem Rady Najwyższej Ukrainy.
zródło:http://pl.wikipedia.org/wiki/Ihor_Ohirko
Całki
Całki
Całka – ogólne określenie wielu różnych, choć powiązanych ze sobą pojęć analizy matematycznej. W artykule rachunek różniczkowy i całkowypodana jest historia ewolucji znaczenia samego słowa całka. Najczęściej przez "całkę" rozumie się całkę oznaczoną lub całkę nieoznaczoną(rozróżnia się je zwykle z kontekstu).
Polskojęzyczny termin został wprowadzony przez Jana Śniadeckiego jako tłumaczenie integral
Całki można sobie wyobrazić jako sumy nieskończenie wielu nieskończenie małych wartości, takich jak np. wartość funkcji pomnożona przez jej nieskończenie małą różniczkę:  (co znajduje odzwierciedlenie w podejściu Riemanna, zob. dalej). Jest to określenie nieścisłe i nieformalne, choć używane w początkach rachunku całkowego przez G. W. Leibniza. Dziś ma ono znaczenie jedynie poglądowe i historyczne, a poszczególne rodzaje całek są definiowane ściśle. Są one szczegółowo opisane w oddzielnych artykułach:
(co znajduje odzwierciedlenie w podejściu Riemanna, zob. dalej). Jest to określenie nieścisłe i nieformalne, choć używane w początkach rachunku całkowego przez G. W. Leibniza. Dziś ma ono znaczenie jedynie poglądowe i historyczne, a poszczególne rodzaje całek są definiowane ściśle. Są one szczegółowo opisane w oddzielnych artykułach:
 (co znajduje odzwierciedlenie w podejściu Riemanna, zob. dalej). Jest to określenie nieścisłe i nieformalne, choć używane w początkach rachunku całkowego przez G. W. Leibniza. Dziś ma ono znaczenie jedynie poglądowe i historyczne, a poszczególne rodzaje całek są definiowane ściśle. Są one szczegółowo opisane w oddzielnych artykułach:
(co znajduje odzwierciedlenie w podejściu Riemanna, zob. dalej). Jest to określenie nieścisłe i nieformalne, choć używane w początkach rachunku całkowego przez G. W. Leibniza. Dziś ma ono znaczenie jedynie poglądowe i historyczne, a poszczególne rodzaje całek są definiowane ściśle. Są one szczegółowo opisane w oddzielnych artykułach:- Całka oznaczona – intuicyjnie: pole powierzchni między wykresem funkcji
 w pewnym przedziale
w pewnym przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , a osią odciętych, wzięte ze znakiem plus dla dodatnich wartości funkcji i minus dla ujemnych. Pojęcie całki oznaczonej, choć intuicyjnie proste, może być sformalizowane na wiele sposobów. Jeśli jakaś funkcja jest całkowalna według dwóch różnych definicji całki oznaczonej, wynik całkowania będzie taki sam.
, a osią odciętych, wzięte ze znakiem plus dla dodatnich wartości funkcji i minus dla ujemnych. Pojęcie całki oznaczonej, choć intuicyjnie proste, może być sformalizowane na wiele sposobów. Jeśli jakaś funkcja jest całkowalna według dwóch różnych definicji całki oznaczonej, wynik całkowania będzie taki sam.- Całka Riemanna, całka Darboux – najprostsze (równoważne ze sobą) definicje całki oznaczonej (zobacz rysunek obok), jednak nie obejmujące wielu ważnych funkcji. Stąd powstało wiele uogólnień tych całek na szerszą klasę funkcji:
- Całka niewłaściwa (Riemanna) – uogólnienie całki Riemanna na niektóre funkcje określone na przedziałach nieskończonych oraz na niektóre funkcje nieograniczone na przedziałach skończonych bądź nie.
- Całka Riemanna-Stieltjesa – uogólnienie całki niewłaściwej, gdy obszarem całkowania nie jest przedział, lecz zbiór wartości pewnej funkcji.
- Całka Russo-Vallois – uogólnienie całki Riemanna-Stieltjesa.
- Całka Riemanna-Stieltjesa – uogólnienie całki niewłaściwej, gdy obszarem całkowania nie jest przedział, lecz zbiór wartości pewnej funkcji.
- Całka niewłaściwa (Riemanna) – uogólnienie całki Riemanna na niektóre funkcje określone na przedziałach nieskończonych oraz na niektóre funkcje nieograniczone na przedziałach skończonych bądź nie.
- Całka Daniella-Stone'a.
- Całka Henstocka-Kurzweila (inne nazwy: całka Denjoy, całka Perrona, całka Denjoy-Perrona).
- Całka Lebesgue'a – najczęściej stosowane uogólnienie całki Riemanna. Rozszerza klasę całkowalnych funkcji jednej zmiennej rzeczywistej. Pozwala także na całkowanie funkcji określonych na innych przestrzeniach mierzalnych i w tym sensie wykracza poza tradycyjne rozumienie całki oznaczonej. Całka Lebesgue'a ma własne uogólnienia i szczególne przypadki:
- całka Lebesgue'a-Stieltjesa – odpowiednik całki Riemanna-Stieltjesa, gdzie funkcja jest całkowana tak jak w całce Lebesgue'a;
- całka Haara – całka Lebesgue'a dla funkcji mierzalnych względem miary Haara, określonej na σ-ciele zbiorów borelowskich lokalnie zwartej grupy topologicznej.
- Całkowanie w przestrzeniach funkcyjnych.
- Całka względem miary wektorowej – całka z funkcji skalarnej względem miary wektorowej.
- Rodzaje całek z funkcji o wartościach wektorowych (np. w przestrzeniach Banacha bądź szerszej klasie przestrzeni):
- całka Pettisa, całka Gelfanda;
- całka Dunforda;
- całka McShane'a;
- całka Bochnera.
- Całka Bartle'a – całka z funkcji o wartościach wektorowych względem miar wektorowych.
- Całka Riemanna, całka Darboux – najprostsze (równoważne ze sobą) definicje całki oznaczonej (zobacz rysunek obok), jednak nie obejmujące wielu ważnych funkcji. Stąd powstało wiele uogólnień tych całek na szerszą klasę funkcji:
- Całka nieoznaczona (albo funkcja pierwotna) – pojęcie odwrotne do pochodnej funkcji (zob. podstawowe twierdzenie rachunku całkowego). Całkę oznaczoną na przedziale
![[a, b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) można też zdefiniować (tzw. całka Newtona-Leibniza) jako różnicę między wartościami całki nieoznaczonej w punktach
można też zdefiniować (tzw. całka Newtona-Leibniza) jako różnicę między wartościami całki nieoznaczonej w punktach  oraz
oraz  . Stąd obliczenie całki nieoznaczonej jest często pierwszym krokiem przy obliczaniu całek oznaczonych.
. Stąd obliczenie całki nieoznaczonej jest często pierwszym krokiem przy obliczaniu całek oznaczonych.- Całka równania różniczkowego – rozwiązanie równania różniczkowego. Jest to uogólnienie całki nieoznaczonej, która także jest rozwiązaniem równania różniczkowego
- gdzie
 jest pierwotną, a
jest pierwotną, a  oznacza całkowaną funkcję.
oznacza całkowaną funkcję.
- Całka równania różniczkowego – rozwiązanie równania różniczkowego. Jest to uogólnienie całki nieoznaczonej, która także jest rozwiązaniem równania różniczkowego
- Całka krzywoliniowa – odpowiednik całki oznaczonej, gdzie obszarem całkowania jest pewna krzywa.
- Całka powierzchniowa – odpowiednik całki oznaczonej, gdzie obszarem całkowania jest pewna powierzchnia, np. pewne koło, albo połowa sfery. Całka krzywoliniowa i całka powierzchniowa to szczególne przypadki całki na hiperpowierzchni. W nowoczesnej teorii całkowania, traktuje się je jako całki Lebesgue'a względem pewnych niezmienniczych miar, określonych na σ-ciałach związanych z daną hiperpowierzchnią.
- Całka podwójna – potocznie: całka z całki (z parametrem). Analogicznie całka potrójna, i ogólnie wielokrotna. Obecnie, całki
 -krotne traktuje się jako całki Lebesgue'a względem
-krotne traktuje się jako całki Lebesgue'a względem  -wymiarowej miary Lebesgue'a.
-wymiarowej miary Lebesgue'a.
- Całka stochastyczna – specjalny rodzaj całki używany w rachunku prawdopodobieństwa. Ma kilka wersji:
- całka Paleya-Wienera (całka Paleya-Wienera-Zygmunda);
- całka Itō – najpowszechniej używana całka stochastyczna;
- całka Stratonowicza – najczęstsza alternatywa dla całki Itō, czasem wygodniejsza.
Niektóre przypadki całek oznaczonych i nieoznaczonych dla pewnych szczególnych funkcji mają własne nazwy:
- całki eliptyczne;
- całka abelowa;
- całka Duhamela (pochodna splotu funkcji);
- całka Fresnela;
- całka Poissona;
- całka wymiany;
- całka J.
sobota, 24 listopada 2012
Pochodne
Pochodna – w analizie matematycznej miara szybkości zmian wartości funkcji względem zmian jej argumentów
Pochodna funkcji zmiennej rzeczywistej o wartościach rzeczywistych
Niech 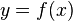 będzie funkcją rzeczywistą zmiennej rzeczywistej
będzie funkcją rzeczywistą zmiennej rzeczywistej  określoną w otoczeniu punktu
określoną w otoczeniu punktu  [2].Pochodną funkcji f(x) w punkcie
[2].Pochodną funkcji f(x) w punkcie  nazywamy granicę (o ile istnieje):
nazywamy granicę (o ile istnieje):
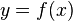 będzie funkcją rzeczywistą zmiennej rzeczywistej
będzie funkcją rzeczywistą zmiennej rzeczywistej  określoną w otoczeniu punktu
określoną w otoczeniu punktu  [2].Pochodną funkcji f(x) w punkcie
[2].Pochodną funkcji f(x) w punkcie  nazywamy granicę (o ile istnieje):
nazywamy granicę (o ile istnieje):
Co symbolicznie zapisuje się w jednej z postaci:
 [3],
[3],
We wzorze tym:
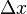 jest przyrostem zmiennej niezależnej x,
jest przyrostem zmiennej niezależnej x, jest przyrostem zmiennej zależnej y,
jest przyrostem zmiennej zależnej y,- Wyrażenie
 nazywa się ilorazem różnicowym; jest on funkcją przyrostu zmiennej niezależnej.
nazywa się ilorazem różnicowym; jest on funkcją przyrostu zmiennej niezależnej.
Jeżeli przyjmie się, że 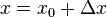 , to pochodną w punkcie
, to pochodną w punkcie  można zapisać następująco:
można zapisać następująco:
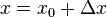 , to pochodną w punkcie
, to pochodną w punkcie  można zapisać następująco:
można zapisać następująco: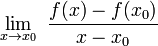 .
.
Często w publikacjach przyrost 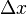 oznacza się literą h. Wtedy pochodna jest równa:
oznacza się literą h. Wtedy pochodna jest równa:
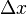 oznacza się literą h. Wtedy pochodna jest równa:
oznacza się literą h. Wtedy pochodna jest równa: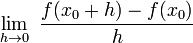 [4].
[4].
Jeśli funkcja 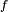 ma pochodną dla każdego elementu swej dziedziny
ma pochodną dla każdego elementu swej dziedziny  to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji
to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji 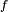 lub krótko: pochodną
lub krótko: pochodną  w dalszej części artykułu będzie ono oznaczane symbolem
w dalszej części artykułu będzie ono oznaczane symbolem  – pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób
– pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób  oznaczać będzie pochodną funkcji
oznaczać będzie pochodną funkcji 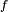 dla argumentu
dla argumentu  w tym wypadku
w tym wypadku  również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
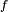 ma pochodną dla każdego elementu swej dziedziny
ma pochodną dla każdego elementu swej dziedziny  to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji
to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji 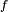 lub krótko: pochodną
lub krótko: pochodną  w dalszej części artykułu będzie ono oznaczane symbolem
w dalszej części artykułu będzie ono oznaczane symbolem  – pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób
– pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób  oznaczać będzie pochodną funkcji
oznaczać będzie pochodną funkcji 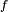 dla argumentu
dla argumentu  w tym wypadku
w tym wypadku  również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.
również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.Własności funkcji pochodne
:iloczyn pochodnej przez stałą,
- pochodną sumy funkcji (addytywność),
 ;
;
- pochodną iloczynu funkcji (reguła Leibniza),
- pochodną złożenia funkcji (reguła łańcuchowa),
- pochodną funkcji odwrotnej,
- pochodną odwrotności funkcji (reguła odwrotności),
- pochodną ilorazu funkcji (reguła ilorazu),
 .
.
Przykłady
funkcje stałe i funkcje potęgowe,Istnieje pewien zestaw funkcji uważanych za elementarne, które wykorzystuje się do obliczania pochodnych bardziej skomplikowanych funkcji i ich złożeń; niech
 oznacza stałą, zaś
oznacza stałą, zaś  będzie liczbą naturalną, wówczas:
będzie liczbą naturalną, wówczas:-
- funkcje wykładnicze[8] i logarytmiczne[9]
- funkcje trygonometryczne[10],
- funkcje cyklometryczne[11],
wszędzie, gdzie powyższe wzory mają sens.
Pochodne wyższego rzędu
Jeżeli pochodna funkcji  i stnieje w każdym punkcie przedziału otwartego (a, b), to otrzymujemy funkcję
i stnieje w każdym punkcie przedziału otwartego (a, b), to otrzymujemy funkcję  , taką że
, taką że
 dla x ∈ (a, b).
dla x ∈ (a, b).
Funkcję tę nazywamy pierwszą pochodną funkcji f. Ta funkcja może być również różniczkowalna w każdym punkcie przedziału (a, b). Różniczkując ją, otrzymujemy drugą pochodną funkcjif:
 dla x ∈ (a, b).
dla x ∈ (a, b).
Oznaczamy to następująco:
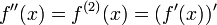 lub
lub  .
.
Ogólnie pochodną rzędu n określamy rekurencyjnie:
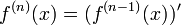 lub
lub  [12].
[12].
Przykłady




- n-tą pochodną iloczynu funkcji można wyrazić za pomocą pochodnych czynników oraz współczynników Newtona wzorem:

Pochodna a monotoniczność funkcji, ekstrema i punkty przegięcia
Z twierdzenia Lagrange'a wynikają następujące własności pochodnej
- Jeżeli funkcja
 jest różniczkowalna, to
jest różniczkowalna, to
- Jeśli
 , to f jest funkcją rosnącą na (a, b).
, to f jest funkcją rosnącą na (a, b). - Jeśli
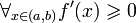 , to f jest funkcją niemalejącą na (a, b).
, to f jest funkcją niemalejącą na (a, b). - Jeśli
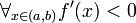 , to f jest funkcją malejącą na (a, b).
, to f jest funkcją malejącą na (a, b). - Jeśli
 , to f jest funkcją nierosnącą na (a, b).
, to f jest funkcją nierosnącą na (a, b). - Jeśli
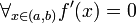 , to f jest funkcją stałą na (a, b).
, to f jest funkcją stałą na (a, b).
- Jeśli
Z własności tych wynika, że ważnymi punktami dziedziny funkcji różniczkowalnej są miejsca zerowe jej pochodnej. Ponieważ funkcja różniczkowalna jest funkcją ciągłą[23], więc jeśli funkcja jest określona na przedziale otwartym, to zbiory rozwiązań nierówności i
i  są sumami przedziałów otwartych.Zbiór miejsc zerowych pochodnej jest zbiorem domkniętym. Miejsca zerowe pierwszej pochodnej są bardzo ważne w badaniu funkcji. W praktyce obliczeniowej funkcje na ogół mają skończoną lub przeliczalną liczbę miejsc zerowych, które dzielą dziedzinę na przedziały otwarte, w których pochodna jest stale dodatnia lub stale ujemna. Wtedy każde miejsce zerowe albo oddziela dwa przedziały, na których pochodna przyjmuje jednakowe znaki, albo różne znaki. Stąd wynikają następujące definicje.
są sumami przedziałów otwartych.Zbiór miejsc zerowych pochodnej jest zbiorem domkniętym. Miejsca zerowe pierwszej pochodnej są bardzo ważne w badaniu funkcji. W praktyce obliczeniowej funkcje na ogół mają skończoną lub przeliczalną liczbę miejsc zerowych, które dzielą dziedzinę na przedziały otwarte, w których pochodna jest stale dodatnia lub stale ujemna. Wtedy każde miejsce zerowe albo oddziela dwa przedziały, na których pochodna przyjmuje jednakowe znaki, albo różne znaki. Stąd wynikają następujące definicje.- Funkcja
 przyjmuje w punkcie x0 maksimum, jeśli istnieje takie otoczenie tego punktu
przyjmuje w punkcie x0 maksimum, jeśli istnieje takie otoczenie tego punktu 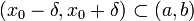 , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 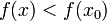 [24].
[24].
Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:- dodatnia w przedziale
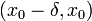 ,
, - równa zero w x0,
- ujemna w przedziale

to funkcja f ma w x0 maksimum.- Funkcja
 przyjmuje w punkcie x0 minimum, jeśli istnieje takie otoczenie tego punktu
przyjmuje w punkcie x0 minimum, jeśli istnieje takie otoczenie tego punktu 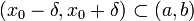 , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność  [25].
[25].
Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:- ujemna w przedziale
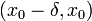 ,
, - równa zero w x0,
- dodatnia w przedziale

to funkcja f ma w x0 minimum.Minima i maksima funkcji nazywamy jej ekstremami.- Funkcja
 ma w punkcie x0 punkt przegięcia, jeśli jej pochodna jest:
ma w punkcie x0 punkt przegięcia, jeśli jej pochodna jest:
- równa zero w x0,
- albo dodatnia, albo ujemna w zbiorze
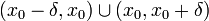 .
.
Schemat badania zmienności funkcji\
Przed narysowaniem wykresu funkcji
 należy[26]:
należy[26]:- Znaleźć dziedzinę funkcji. Znaleźć granice funkcji w punktach brzegu dziedziny.
- Znaleźć miejsca zerowe pochodnej funkcji, punkty, w których pochodna funkcji nie istnieje lub jest równa ±∞. Obliczyć wartości funkcji w tych punktach i stwierdzić, czy w tych punktach funkcja przyjmuje minimum lub maksimum.
- Na każdym z przedziałów wyznaczonych przez miejsca zerowe pochodnej ustalić, czy funkcja jest rosnąca, czy malejąca.
- Zbadać istnienie punktów przegięcia funkcji.
- Rozwiązać, jeśli to możliwe, równanie
 oraz ustalić przedziały, w których funkcja ma stały znak.
oraz ustalić przedziały, w których funkcja ma stały znak. - Znaleźć asymptoty funkcji.
Funkcje wielu zmiennych
Pochodne cząstkowe
W przypadku funkcji wielu zmiennych
 możliwe jest ustalenie
możliwe jest ustalenie  jej argumentów i traktowanie jej jako funkcji jednej zmiennej – pochodną względem tej zmiennej nazywa się „pochodną cząstkową”. Jeśli
jej argumentów i traktowanie jej jako funkcji jednej zmiennej – pochodną względem tej zmiennej nazywa się „pochodną cząstkową”. Jeśli  gdzie
gdzie  to pochodną cząstkową funkcji
to pochodną cząstkową funkcji 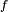 względem jej
względem jej  -tej współrzędnej
-tej współrzędnej  nazywa się wartość granicyo ile istnieje i jest skończona. W zapisie wektorowym powyższą granicę można zapisać wzoremgdzie
nazywa się wartość granicyo ile istnieje i jest skończona. W zapisie wektorowym powyższą granicę można zapisać wzoremgdzie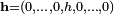 jest wektorem o jedynej niezerowej współrzędnej
jest wektorem o jedynej niezerowej współrzędnej  -tej.Powyższą definicję można rozszerzyć zauważając, że
-tej.Powyższą definicję można rozszerzyć zauważając, że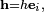 gdzie
gdzie  jest wektorem bazy standardowej przestrzeni
jest wektorem bazy standardowej przestrzeni 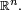 Wybranie dowolnego wektora jednostkowego
Wybranie dowolnego wektora jednostkowego  zamiast wektora bazy prowadzi do definicji pochodnej kierunkowej wzdłuż
zamiast wektora bazy prowadzi do definicji pochodnej kierunkowej wzdłuż  mianowicie:Jeśli
mianowicie:Jeśli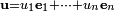 jest wektorem jednostkowym, to pochodna kierunkowa funkcji
jest wektorem jednostkowym, to pochodna kierunkowa funkcji 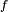 wzdłuż
wzdłuż  jest równa kombinacji liniowej pochodnych cząstkowych funkcji
jest równa kombinacji liniowej pochodnych cząstkowych funkcji 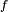 o współczynnikach
o współczynnikach 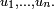
Pochodne zupełne
 W czerwonym punkcie paraboloidyfunkcja
W czerwonym punkcie paraboloidyfunkcja
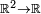 ją opisująca przyjmujemaksimum: warunkiem koniecznym jego istnienia jest znikanie pochodnej (w słabym/silnym sensie) wspomnianej funkcji.Dowolną funkcję
ją opisująca przyjmujemaksimum: warunkiem koniecznym jego istnienia jest znikanie pochodnej (w słabym/silnym sensie) wspomnianej funkcji.Dowolną funkcję można rozłożyć na funkcje współrzędnych
można rozłożyć na funkcje współrzędnych  przyjmując
przyjmując 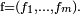 Jeżeli funkcje te są różniczkowalne w każdym kierunku, co jest równoważne istnieniu ich wszystkich pochodnych cząstkowych, to funkcję
Jeżeli funkcje te są różniczkowalne w każdym kierunku, co jest równoważne istnieniu ich wszystkich pochodnych cząstkowych, to funkcję  nazywa się różniczkowalną w słabym sensie[27]; przedstawieniem tej pochodnej we współrzędnych za pomocą odpowiadającej jej macierzy przekształcenia liniowego jest tzw.macierz Jacobiego.Mogłoby się wydawać, że definicja słabej pochodnej jest w zupełności zadowalająca, jednak w przypadku funkcji wielowymiarowych należy zwrócić uwagę na zjawiska związane z większą liczbą wymiarów: istnieją przykładowo funkcje, które mają pochodne we wszystkich kierunkach (równoważnie: mają wszystkie pochodne cząstkowe, zob. ostatni ustęp poprzedniej sekcji), czyli wzdłuż prostych, lecz nie mają pochodnych wzdłuż innych krzywych – problem ten nie istnieje w przypadku funkcji zmiennej rzeczywistej, gdzie granicę można obliczać wyłącznie wzdłuż krzywych leżących wyłącznie na prostej.Definicja pochodnej funkcji wielu zmiennych
nazywa się różniczkowalną w słabym sensie[27]; przedstawieniem tej pochodnej we współrzędnych za pomocą odpowiadającej jej macierzy przekształcenia liniowego jest tzw.macierz Jacobiego.Mogłoby się wydawać, że definicja słabej pochodnej jest w zupełności zadowalająca, jednak w przypadku funkcji wielowymiarowych należy zwrócić uwagę na zjawiska związane z większą liczbą wymiarów: istnieją przykładowo funkcje, które mają pochodne we wszystkich kierunkach (równoważnie: mają wszystkie pochodne cząstkowe, zob. ostatni ustęp poprzedniej sekcji), czyli wzdłuż prostych, lecz nie mają pochodnych wzdłuż innych krzywych – problem ten nie istnieje w przypadku funkcji zmiennej rzeczywistej, gdzie granicę można obliczać wyłącznie wzdłuż krzywych leżących wyłącznie na prostej.Definicja pochodnej funkcji wielu zmiennych stanowiącą rozwiązanie tego problemu naśladuje definicję „różniczkową” dla funkcji rzeczywistej (zob.Związek z różniczką). Pochodną w mocnym sensie[28] funkcji
stanowiącą rozwiązanie tego problemu naśladuje definicję „różniczkową” dla funkcji rzeczywistej (zob.Związek z różniczką). Pochodną w mocnym sensie[28] funkcji  dla argumentu punktowego
dla argumentu punktowego 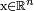 nazywa się takie przekształcenie liniowe
nazywa się takie przekształcenie liniowe  dla którego zachodzigdzie
dla którego zachodzigdzie oznacza moduł odpowiednich wektorów; odwzorowanie
oznacza moduł odpowiednich wektorów; odwzorowanie  podobnie jak w przypadku jednowymiarowym, nazywa się różniczką (w mocnym sensie) funkcji
podobnie jak w przypadku jednowymiarowym, nazywa się różniczką (w mocnym sensie) funkcji  [29]. Rolę funkcji pochodnej pełni tu więc odwzorowanie
[29]. Rolę funkcji pochodnej pełni tu więc odwzorowanie  przestrzeni współrzędnych w przestrzeń liniową przekształceń liniowych (por. przestrzeń funkcyjna przekształceń liniowych) dane wzorem
przestrzeni współrzędnych w przestrzeń liniową przekształceń liniowych (por. przestrzeń funkcyjna przekształceń liniowych) dane wzorem  tj. przypisujące punktowi przekształcenie liniowe.Istnienie pochodnej w silnym sensie pochodnej pociąga istnienie pochodnej w słabym sensie; jeżeli jednak funkcja jest różniczkowalna w słabym sensie i wszystkie jej pochodne cząstkowe (kierunkowe) są ciągłe, to funkcja jest różniczkowalna w silnym sensie w sposób ciągły (tzn. jest klasy
tj. przypisujące punktowi przekształcenie liniowe.Istnienie pochodnej w silnym sensie pochodnej pociąga istnienie pochodnej w słabym sensie; jeżeli jednak funkcja jest różniczkowalna w słabym sensie i wszystkie jej pochodne cząstkowe (kierunkowe) są ciągłe, to funkcja jest różniczkowalna w silnym sensie w sposób ciągły (tzn. jest klasy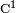 ). Oba rodzaje pochodnych mają wiele własności pochodnej funkcji rzeczywistej, np.liniowość, czy zachodzenie reguły łańcuchowej. Bezpośrednie generalizacje pojęć pochodnych w słabym/silnym sensie, tj. pochodne Gâteaux/Frécheta, opisano w Uogólnieniach.zródło: http://pl.wikipedia.org/wiki/Pochodna
). Oba rodzaje pochodnych mają wiele własności pochodnej funkcji rzeczywistej, np.liniowość, czy zachodzenie reguły łańcuchowej. Bezpośrednie generalizacje pojęć pochodnych w słabym/silnym sensie, tj. pochodne Gâteaux/Frécheta, opisano w Uogólnieniach.zródło: http://pl.wikipedia.org/wiki/Pochodna- Jeżeli funkcja
Subskrybuj:
Posty (Atom)